Fractions can be confusing. But there there are a few simple rules which encompass everything you could ever want to do with fractions. In order to use the fraction rules, you have to be able to add, subtract, and multiply ordinary whole numbers. You’ll also want to keep in mind two rules about arithmetic which are very helpful with fractions.
Arithmetic Rule #1
Any number stays the same when zero is added to it or subtracted from it.

Arithmetic Rule #2
Any number stays the same when multiplied or divided by one.
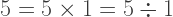
Fractions have a few specific terms which are important to know as well. Here are the big ones:
Glossary
- numerator: the number on the top of a fraction
- denominator: the number on the bottom of a fraction
- improper fraction: a fraction with a larger numerator than denominator
- reduced fraction: a fraction that cannot be equivalently written with smaller numerator and denominator
- mixed fraction: a fraction with a whole number part and a fractional part
On to the rules, of which there are six, but only the last two are particularly interesting.
Fraction Rule #1
Any fraction with  as the denominator is undefined (illogical, nonsense, error).
as the denominator is undefined (illogical, nonsense, error).

Fraction Rule #2
Any fraction with the same number for both numerator and denominator is equal to  .
.
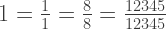
Fraction Rule #3
Any fraction with  as the numerator is equal to
as the numerator is equal to  (unless the denominator is also
(unless the denominator is also  - see rule #1).
- see rule #1).

Fraction Rule #4
Any simple number can be converted to a fraction by placing it over  .
.

This is the same as the division version of arithmetic rule #2, since fractions are just division problems.
Fraction Rule #5
Fractions with the same denominator are added by adding their numerators and copying the denominator. Fractions with different denominators cannot be added together directly (see below).
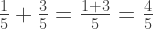
Fraction Rule #6
Fractions can be multiplied by multiplying the numerators and denominators separately.

Using the Rules
Division
Division is often a useful thing to do with fractions, and it’s easy. Just turn the divisor fraction (the second one) upside-down and multiply. This is commonly referred to as “invert and multiply”.

Improper Fractions
Improper fractions can be made proper by repeatedly pulling  (expressed as a fraction) out of the fraction to create a proper mixed fraction. Remember that every fraction has a “ones” place to the left of the actual fraction to make it a mixed fraction.
(expressed as a fraction) out of the fraction to create a proper mixed fraction. Remember that every fraction has a “ones” place to the left of the actual fraction to make it a mixed fraction.

The  that we want to pull out when converting an improper fraction to proper form is based on the denominator. By addition rule #1, we can subtract
that we want to pull out when converting an improper fraction to proper form is based on the denominator. By addition rule #1, we can subtract  from something without changing it. And we know that a fraction with the same numerator and denominator is equal to
from something without changing it. And we know that a fraction with the same numerator and denominator is equal to  by fraction rule #2. So if we subtract a one-equivalent fraction and then add
by fraction rule #2. So if we subtract a one-equivalent fraction and then add  back to it, it won’t have changed.
back to it, it won’t have changed.

In this case we still have an improper fraction, so we’ll repeat the process again (and continue until we no longer have an improper fraction).

So the improper fraction 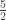 reduces to the proper mixed fraction
reduces to the proper mixed fraction 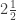 .
.
Mixed Fractions
Sometimes you have a mixed fraction and want to make it a pure improper fraction. Get rid of that pesky whole number part. Improper fractions are usually easier to manipulate than mixed fractions, so it’s common to make everything improper, solve the problem, and then make the answer proper again.
The process of converting a mixed fraction to an improper fraction is quite simple. Remember that a mixed fraction is the same as the fractional part plus the whole number part.

If the whole number is converted to a fraction, we can just add them and get a fractional result. We know how to do that because rule #4 says we can slap a  under any whole number. The denominators won’t match, but arithmetic rule #2 says we can multiply by
under any whole number. The denominators won’t match, but arithmetic rule #2 says we can multiply by  (a special form – namely the denominator over it self – see rule #2) without affecting anything.
(a special form – namely the denominator over it self – see rule #2) without affecting anything.

This process is a special case of adding fractions with different denominators discussed next.
Adding Fractions With Different Denominators
Adding fractions with different denominators requires multiplying one or both fractions by a special form of  first (which doesn’t change anything – see arithmetic rule #2). The trick is in picking the right version of
first (which doesn’t change anything – see arithmetic rule #2). The trick is in picking the right version of  to use. The goal is to get both fractions to have the same denominator. The easiest way is to multiply each fraction by the denominator of the other fraction over itself (which is a way of writing
to use. The goal is to get both fractions to have the same denominator. The easiest way is to multiply each fraction by the denominator of the other fraction over itself (which is a way of writing  – see fraction rule #2). For the problem
– see fraction rule #2). For the problem

we want to do this

Doing multiplication according to rule #6 yields this

Now that the denominators match (and they always will by following this process) we can add according to rule #5 without difficulty.

An there we go, adding two fractions with different denominators by multiplying the parts by a clever form of  .
.
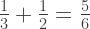
Reducing Fractions (Part 1)
Answers to problems, whether in math class or the real world, should almost always be given in reduced fractions. No one likes to be told  when they ask how much pizza is left. Much better is
when they ask how much pizza is left. Much better is 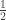 , but how to get from one to the other?
, but how to get from one to the other?
Since you know that the above rules describe everything you’ll need to do with fractions, it’s probably not surprising that a special form of  is integral to the answer. Finding the right form is tricker than for addition above, but there is still a foolproof process.
is integral to the answer. Finding the right form is tricker than for addition above, but there is still a foolproof process.
The first step is to find a non-trivial common factor for the numerator and denominator. A factor is a number that can be multiplied by another number to get the answer. For example,  and
and  are two factors of
are two factors of 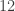 . The “non-trivial” means “not including one” since that’s a factor of every number and per addition rule #2 and fraction rule #4 dividing by
. The “non-trivial” means “not including one” since that’s a factor of every number and per addition rule #2 and fraction rule #4 dividing by  doesn’t change anything. We don’t want just any non-trivial factor, however, we need one that is a factor of both the numerator and the denominator (a common factor).
doesn’t change anything. We don’t want just any non-trivial factor, however, we need one that is a factor of both the numerator and the denominator (a common factor).
factors of 5: 1, 5
factors of 10: 1, 2, 5, 10
Since 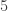 is prime, the only options are
is prime, the only options are  and itself.
and itself.  has a couple more options, but the only non-trivial common factor of both numerator and denominator is
has a couple more options, but the only non-trivial common factor of both numerator and denominator is 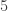 . If you’re reducing a fraction and there are multiple choices for common factors, always pick the largest one. If you don’t pick the largest one, when you’re done, you only have a partially reduced fraction, not a fully reduced one (and you’ll have to do the process again). If there aren’t any non-trivial common factors, meaning
. If you’re reducing a fraction and there are multiple choices for common factors, always pick the largest one. If you don’t pick the largest one, when you’re done, you only have a partially reduced fraction, not a fully reduced one (and you’ll have to do the process again). If there aren’t any non-trivial common factors, meaning  is the only common factor, then the fraction is already in it’s reduced form.
is the only common factor, then the fraction is already in it’s reduced form.
Now that we have 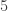 as our factor, we can rewrite our problem by “pulling out” that factor according to rule #6:
as our factor, we can rewrite our problem by “pulling out” that factor according to rule #6:

Thus we know that 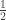 is a reduced version of
is a reduced version of  . Further, since
. Further, since 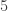 was the largest common factor, we know that it cannot be reduced any further.
was the largest common factor, we know that it cannot be reduced any further.
Reducing Fractions (Part 2)
A quick way of describing the above process is to say “divide the same number out of top and bottom and repeat you can’t do it anymore”. It’s still the same process, but mashing a few steps together and not worrying so much about doing it all in one pass. As an example, reduce  . Top and bottom are both even, so let’s divide out
. Top and bottom are both even, so let’s divide out  .
.

Still not reduced, but  will divide out of each.
will divide out of each.

Alright, no other numbers can be divided out, so it must be reduced. If we’d picked 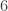 (
( ) initially, we’d have been done in one step, because
) initially, we’d have been done in one step, because 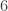 is the largest common factor of
is the largest common factor of 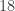 and
and  as discussed above. Doing it this way meant we had to go through the process a couple times, but we didn’t have to figure out the list of factors and then figure out the largest common factor.
as discussed above. Doing it this way meant we had to go through the process a couple times, but we didn’t have to figure out the list of factors and then figure out the largest common factor.
Both approaches are 100% correct and will yield the same result every time. If you’re doing the reduction in your head while baking, chances are you’ll do the quick’n’dirty way. If you’re doing the reduction while designing a bridge strut, you’ll probably do it the longer way. Regardless which you choose, the answer will be the same.
Reducing Proper and Improper Fractions
Reducing fractions and switching from proper and improper forms are all simple conversions. They’re not changing the fraction’s value, just the way it’s written. Thus if you have to do both, it’s completely irrelevant which order you do them.
Since a proper fraction’s whole number part is always reduced (whole numbers are as reduced as they come), doing the reduction second is often easier because the numbers in the fraction will be smaller. But it doesn’t change the math at all; the result is the same.
